Stochastic Volatility and Fourier Transformation
(2 SWS)
If your are interested and want to join please contact Prof. Günther or Prof. Ehrhardt.
In this seminar we consider Fourier Transform Methods applied to Option Pricing problems. We consider a real valued random variable X and consider the expectation
![[ ] ∫
φX (u ) := E eiuX = eiuX dℙX ,](aushang1x.png) | (1) |
where i denotes the imaginary unit, i.e. i =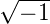 
. If the distribution 
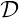X of X has a
density with respect to Lebesgue measure, denoted by fX(x), this expectation can be
written as
 |
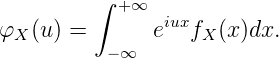In this seminar we consider the Heston model that is specified by the following system of Stochastic Differential equations:
| dS(t) | = μ(t)dt + σ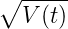(t) dW(t), | (2) | |
| dV (t) | = κ(t)(θ(t) - V (t))dt + ν(t)dZ(t), | (3) | |
| ⟨W(t),Z(t)⟩ | = ρ(t)dt, | ||
| S(0) | = S0, | ||
| V (0) | = V 0, |
where W and Z are correlated Brownian motions and the quantity ρ is called the correlation. Furthermore, κ the mean reversion, θ the long term mean, ν the volatility of variance. The spot asset value is S0 and the spot variance value is V 0.
Given a strike price K and a maturity T for option pricing problems we would be interested in quantities such as ℙ(S(T) ≤ K) or ℙ(S(T) ≥ K). This would enable us to assign a probability to the event that at time T is asset is above or below the strike price and, thus, a Call, resp. Put option is exercised or not.
The bad news here is that the probability distribution, nor the density, of S is not available in closed form and, thus, pricing an option using the above mentioned probabilities and using a Black-Scholes-Merton type formula is not possible. However, for a lot of models including the Heston model the characteristic function which is nothing but the Fourier transform of the probability density is available in closed form. Furthermore, it comes in handy that a mathematical theorem is available that relates the probability density/distribution to the characteristic function – called the Gil-Pelaez inversion. It holds that
 |
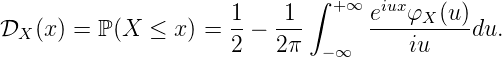In this seminar we will understand the notion of the Fourier transform, study the basic properties and prove the Gil-Pelaez theorem. Equipped with the results we wish to start digging into the practical aspects of using Fourier transforms for option pricing. After understanding the different methods proposed in the literature we wish to implement the methods in Matlab/VBA and apply the methods for pricing and calibration. There is already code available, e.g. Kienitz, Wetterau (2012).
We aim to have all presentations on a single day. The presentations will be held at our industry partner locations. In this case it is Talanx Asset Management. Talanx is a Cologne based asset manager and is located near the station Cologne Deutz.
We base the practical part on the following books, papers, code repositories.
It is determined at the beginning of the seminar how the practical part is structured an what is expected from the presenter.
Note: It is essential that you not only copy and paste the code but fulfill a specific task that is agreed on before you prepare your topic and your presentation.
We base the presentations on the following papers: