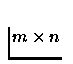2.2.0.0.3 Matrices

Row elements are separated by commas or spaces and column elements by semi-colons. Multiplication of matrices by scalars, vectors, or other matrices is in the usual sense. Addition and subtraction of matrices is element-wise and element-wise multiplication and division can be accomplished with the .* and ./ operators.

 
--> A=[2 1 4;5 -8 2]
 A         =
 
!   2.    1.    4. !
!   5.  - 8.    2. !
 
--> b=ones(2,3)
 b         =
 
!   1.    1.    1. !
!   1.    1.    1. !
 
--> A.*b
 ans       =
 
!   2.    1.    4. !
!   5.  - 8.    2. !
 
--> A*b'
 ans       =
 
!   7.    7. !
! - 1.  - 1. !

Notice that the ones   operator with two real numbers as arguments separated by a comma creates a matrix of ones using the arguments as dimensions (same for zeros). Matrices can be used as elements to larger matrices . Furthermore, the dimensions of a matrix can be changed.

 
--> A=[1 2;3 4]
 A         =
 
!   1.    2. !
!   3.    4. !
 
--> B=[5 6;7 8];
 
--> C=[9 10;11 12];
 
--> D=[A,B,C]
 D         =
 
!   1.    2.    5.    6.    9.     10. !
!   3.    4.    7.    8.    11.    12. !
 
--> E=matrix(D,3,4)
 E         =
 
!   1.    4.    6.    11. !
!   3.    5.    8.    10. !
!   2.    7.    9.    12. !

-->F=eye(E)
 F  =
 
!   1.    0.    0.    0. !
!   0.    1.    0.    0. !
!   0.    0.    1.    0. !
 
-->G=eye(4,3)
 G  =
 
!   1.    0.    0. !
!   0.    1.    0. !
!   0.    0.    1. !
!   0.    0.    0. !

Notice that matrix D is created by using other matrix elements. The matrix  primitive creates a new matrix E with the elements of the matrix D using the dimensions specified by the second two arguments. The element ordering in the matrix D is top to bottom and then left to right which explains the ordering of the re-arranged matrix in E.

The function eye creates an 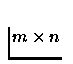$m\times n$ matrix with 1 along the main diagonal (if the argument is a matrix E , m and n are the dimensions of E ) .

Sparse constant matrices are defined through their nonzero entries (type help sparse for more details). Once defined, they are manipulated as full matrices.