|
Bergische Universität Wuppertal
|
|
|
|
|
Bergische Universität Wuppertal
|
|
|
[click to enlarge] |
 |
Wave Propagation in Periodic MediaAnalysis, Numerical Techniques and practical ApplicationsMatthias Ehrhardt (ed.)E-Book Series Progress in Computational Physics (PiCP), Volume 1Bentham Science Publishers, June 2010.Book Webpage at Publisher |
|
[click to enlarge] |
 |
 |
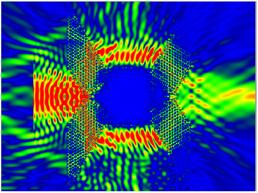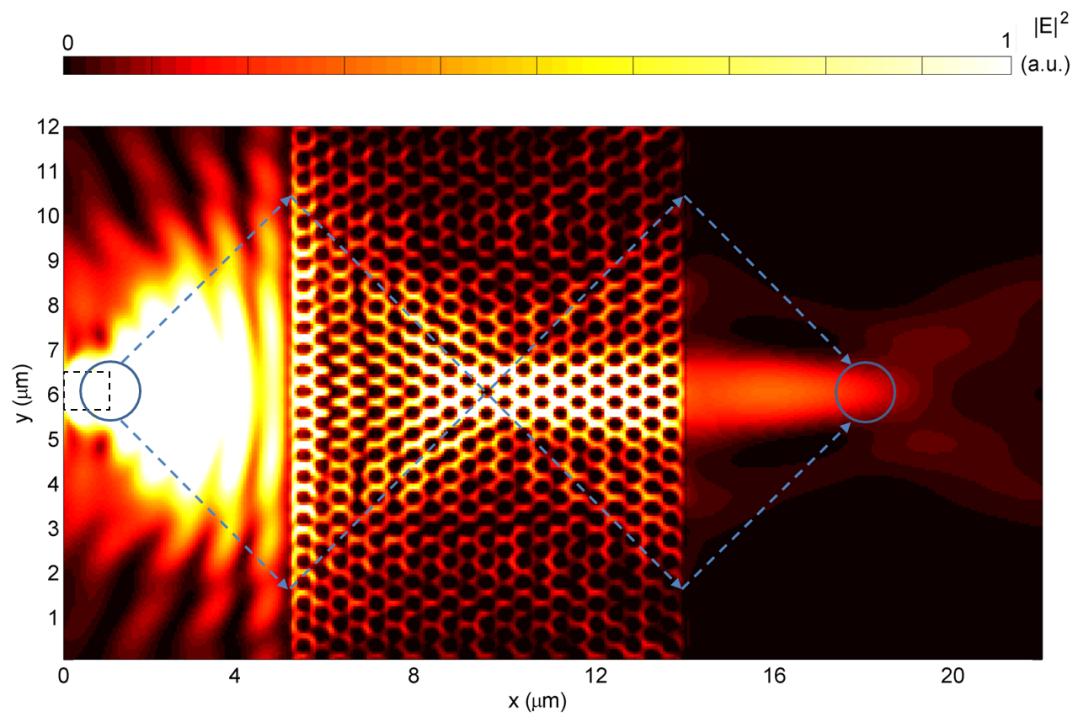
Left figure: 2D FDTD simulation of photonic crystal (PC)
based optical cloaking at 1.55 μm. Right figure:
3D FDTD simulation of focusing using a photonic crystal based flat lens
at 1.55 μm. Pictures are courtesy of Olivier Vanbésien, IEMN Lille, France. |
|
 |
Subject: Nowadays periodic structure problems arise quite often in many modern application areas like semiconductor nanostructures (e.g. quantum dots and nanocrystals), semiconductor superlattices, photonic crystals structures, meta materials or Bragg gratings of surface plasmon polariton waveguides.
This first volume treats both, mathematical analysis of periodic structure problems and state-of-the art numerical techniques, like frequency domain methods , beam propagation methods and eigenmode expansion methods. Several chapters are devoted to concrete applications of periodic media simulations, E.g. in optical applications these periodic media, have the special capability to select the ranges of frequencies of the waves that are allowed to pass or blocked in the waveguide and act as an efficient frequency filter.
Purpose: The purpose of this book is to give an overview on the current state-of-the-art research on periodic structure problems.
The book is designed to be consisting of a collection of contributed chapters. Outstanding experts working successfully in this challenging research area will be invited to contribute each a chapter of roughly 30-40 pages to this volume.
Academic Level: The principal audience is Ph.D. students and lecturer of computational physics and numerical mathematics.
by Olivier Vanbésien, IEMN Lille, France.
Wave Propagation in Periodic Media, (2 pages)
by Matthias Ehrhardt, Lehrstuhl für Angewandte Mathematik und Numerische Mathematik, Fachbereich Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, Wuppertal, Germany.
by Nikolai Bagraev, A.F. Ioffe Physico-Tecnical Institute, St. Petersburg, Russia.
and Gaven Martin, Massey University, Albany, Auckland: NZ Institute for Advanced study, New Zealand.
and Boris Pavlov, Massey University, Albany, Auckland: NZ Institute for Advanced study, New Zealand.
V.A. Fock Institute for Physics of St.-Petersburg University, Petrodvorets, Russia.
Abstract: The dynamics of a single electron is considered on a periodic square lattice constructed of rhomboidal quantum wells interacting via narrow links. The spectral structure of bands and gaps of the lattice is derived from an accurate analysis of Bloch waves, based on DN- maps of the quantum wells. For periodic lattice with rhomboidal periods, a solvable model, is constructed based on a rational approximation of DtN-maps of the quantum wells by establishing a communication between them via partial boundary conditions emulating the covalent bonds.
In the case of the corresponding double periodic lattice, the weak interaction of the two parallel periodic quasi-2d sub-lattices defines, due to the 2d Landau-Zener effect, a high mobility of the corresponding charge carriers in certain direction on the quasi-momenta plane.
by Stephen P. Shipman, Department of Mathematics, Louisiana State University, Baton Rouge, USA.
Abstract: This chapter concerns the interaction between guided electromagnetic or acoustic modes of a penetrable periodic planar waveguide and plane waves originating from sources exterior to the waveguide. The interaction causes resonant enhancement of fields in the waveguide and anomalous transmission of energy across it. A guided mode is an eigenfunction of a member of the family of operators in the Floquet-Bloch decomposition of the periodic differential operator underlying the waveguide structure. The theory of existence or nonexistence of modes in ideal lossless waveguides is founded on variational principles. The mechanism for resonant scattering behavior is the dissolution of an embedded eigenvalue into the continuous spectrum, which corresponds to the destruction of a guided mode of a waveguide, upon perturbation of the wavevector or the material properties or geometry of the structure. Analytic perturbation of functions that unify the guided modes and the extended scattering states gives rise to asymptotic formulas for transmission anomalies.
by Johannes Tausch, Department of Mathematics, Southern Methodist University, Dallas, Texas, USA.
Abstract: The propagation of electromagnetic waves in dielectric slab waveguides with periodic corrugations is described by the spectrum of the Helmholtz operator on an infinite strip with quasiperiodic boundary conditions. This chapter reviews the basic properties of this spectrum, which typically consists of guided modes, radiation modes and leaky modes. A great deal of attention will be devoted to planar waveguides which share some of the important features of the periodic case. To compute the eigenmodes and the associated propagation constants numerically, one usually truncates the domain that contains the grating and imposes certain radiation conditions on the artificial boundary. An alternative to this approach is to decompose the infinite strip into a rectangle, which contains the grating, and two semi-infinite domains. The guided and leaky modes can be computed by matching the Dirichlet-to-Neumann operator on the interfaces of these three domains. The discretized eigenvalue problem is nonlinear because of the appearance of the propagation constant in the artificial boundary condition. We will discuss how such problems can be solved by numerical continuation. In this approach, one starts with an approximating planar waveguide and then follows the solutions by a continuous transition to the multilayer periodic structure. The chapter is concluded with a brief description of how the perfectly matched layer can be used to compute the guided modes of a waveguide.
by Xavier Antoine, Institut Elie Cartan Nancy (IECN), Université Henri Poincaré Nancy 1, Nancy, France.
and Christophe Geuzaine, University of Liège, Department of Electrical Engineering and Computer Science, Montefiore Institute, Liège, France.
and Karim Ramdani, INRIA (CORIDA Team) & Institut Elie Cartan Nancy (IECN), Université Henri Poincaré Nancy 1, Nancy, France.
Abstract: The aim of this chapter is to explain some recent numerical methods for solving high-frequency scattering problems. Most particularly, we focus on the multiple scattering problem where rays are multiply bounced by a collection of separate objects. We review recent developments for three main families of approaches: Fourier series based methods, Partial Differential Equations approaches and Integral Equations based techniques. Furthermore, for each of these three families of methods, we present original procedures for solving the high-frequency multiple scattering problem. Computational examples are given, in particular for finite periodic structures calculations. Difficulties for solving such problems are explained, showing that many serious simulation problems are still open.
by Sonia Fliss, Applied Mathematics Department, ENSTA, Paris, France,
and Patrick Joly, Applied Mathematics Department, ENSTA, Paris, France
and Jing-Rebecca Li, INRIA POEMS Project, Rocquencourt, Le Chesnay Cedex, France.
Abstract: We present in this chapter a review of some recent research work about a new approach to the numerical simulation of time harmonic wave propagation in infinite periodic media including a local perturbation. The main difficulty lies in the reduction of the effective numerical computations to a bounded region enclosing the perturbation. Our objective is to extend the approach by Dirichlet-to-Neumann (DtN) operators, well known in the case of homogeneous media (as non local transparent boundary conditions).
The new difficulty is that this DtN operator can no longer be determined explicitly and has to be computed numerically. We consider successively the case of a periodic waveguide and the more complicated case of the whole space. We show that the DtN operator can be characterized through the solution of local PDE cell problems, the use of the Floquet-Bloch transform and the solution of operator-valued quadratic or linear equations.
In our text, we shall outline the main ideas without going into the rigorous mathematical details. The non standard aspects of this procedure will be emphasized and numerical results demonstrating the efficiency of the method will be presented.
by Matthias Ehrhardt, Lehrstuhl für Angewandte Mathematik und Numerische Mathematik, Fachbereich Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, Wuppertal, Germany.
and Chunxiong Zheng, Department of Mathematical Sciences, Tsinghua University, Beijing, China.
Abstract: Nowadays periodic media problems widely exist in in many modern application areas like semiconductor nanostructures (e.g.\ quantum dots and nanocrystals), semi-conductor superlattices, photonic crystals (PC) structures, meta materials or Bragg gratings of surface plasmon polariton (SPP) waveguides, etc. Often these problems are modeled by partial differential equations with periodic coefficients and/or periodic geometries. In order to numerically solve these periodic structure problems efficiently one usually confines the spatial domain to a bounded computational domain (i.e. in a neighborhood of the region of physical interest). Hereby, the usual strategy is to introduce so-called artificial boundaries and impose suitable boundary conditions. For wave-like equations, the ideal boundary conditions should not only lead to well-posed problems, but also mimic the perfect absorption of waves traveling out of the computational domain through the artificial boundaries.
In the first part of this chapter we prove a novel analytical impedance expression for general second order ODE problems with periodic coefficients. This new expression for the kernel of the Dirichlet-to-Neumann mapping of the artificial boundary conditions is then used for computing the bound states of the Schrödinger operator with periodic potentials at infinity. Other potential applications are associated with the exact artificial boundary conditions for some time-dependent problems with periodic structures. As an example, a two-dimensional hyperbolic equation modeling the TM polarization of the electromagnetic field with a periodic dielectric permittivity is considered.
In the second part of this chapter we present a new numerical technique for solving periodic structure problems. This novel approach possesses several advantages. First, it allows for a fast evaluation of the Robin-to-Robin operator for periodic array problems. Secondly, this computational method can also be used for bi-periodic structure problems with local defects. Our strategy is an improvement of the recently developed recursive doubling process by Yuan and Lu. In the sequel we consider several problems, such as the exterior elliptic problems with strong coercivity, the time-dependent Schrödinger equation and the Helmholtz equation with damping.
Finally, we conclude this chapter with a concise discussion of the challenging case when the wavenumber lies in the passbands.
by Olivier Vanbésien, Institut d'Electronique, de Microélectronique et de Nanotechnologie, Université des Sciences et Technologies de Lille, France.
Abstract: In this chapter, we will address the potential applications of negative refraction in artificial periodic media. Different approaches will be considered depending on the targeted wavelength operation from microwaves down to optics.
First, physical concepts to create such an abnormal propagation regime will be described:Second, practical examples of real devices will be given, starting from negative refraction evidence in a two dimensional prism in microwaves, backward wave propagation in a periodically loaded transmission line to end with subwavelength focusing by a photonic crystal slab for optical waves.
- negative permittivity and negative permeability engineering in patterned metallic or metallo-dielectric structures namely metamaterials
- band structure engineering in full dielectric structures namely photonic crystals
In a third part, other exciting properties beyond negative refraction will be evoked with the design of hyperlenses and cloaking devices.
by Günter Leugering, Lehrstuhl für Angewandte Mathematik II, Universität Erlangen-Nürnberg, Germany,
Eduard Rohan, New Technologies Research Center, Research Institute at University of West Bohemia, Plzen, Czech Republic
and Frantisek Seifrt, Lehrstuhl für Angewandte Mathematik II, Universität Erlangen-Nürnberg, Germany.
Abstract: This chapter deals with electromagnetic waves propagating through periodically heterogeneous layer, involving dielectrics and conductors. The aim of the chapter is to develop homogenized transmission conditions as the limit of the model featured by small parameter ε which tends to zero and, in reverse, to determine the optimal structure of the periodic cells with respect to desired material properties as in meta-materials.
We consider a layer with the thickness proportional to ε embedding materials with different permitivities and conductivities; the structure is formed by fibrous graining and is ε-periodic w.r.t. the fiber-orthogonal tangential direction of the layer's mid-surface. The electromagnetic field is described by electric Hertz potential, thus the system of the Maxwell equations reduces to the Helmholtz-type equation with heterogeneous, complex elliptic operator.
We discuss two types of the boundary conditions prescribed on the upper and lower faces of the layer:We apply the two-scale homogenization method (periodic unfolding) to pass to the limit for ε→0 in the weak formulation of the scattering problem. As the output transmission conditions on the limit layer mid-surface are obtained in an implicit form, involving the jump in the scattered fields and an internal variable associated with field distribution in the layer.
- the Robin type condition respecting amplitudes of the incident, reflected and transmitted wave
- the Neumann type condition related to the circulation of the magnetic induction
The limit transmission conditions are then intended for optimal control in the inverse scattering problem. We discuss how the material composition of the layer influences the reflection and transmission of the scattered fields.
|