
|
Bergische Universität Wuppertal
|

|
|

|
Bergische Universität Wuppertal
|

|
|
Project: Research Program EPEAEK - Archimedes IIINew numerical and computational methods for the solution of differential equations with applications in environmental issuesfinanced by The European Union & The Ministry of Education, Lifelong Learning and Religious Affairs of Greece(01/2012 - 08/2014)
|
The need of accurate local predictions of environmental parameters has increased significantly in recent years as a result of the large number of social and commercial activities that are directly affected. The validity of such data is particularly important in terms of renewable energy for the safe assessment of available energy resources in wind farms and off shore platforms.
On European level, the previous requirements have led to the activation of numerous research and operational centers that develop high quality scientific tools able to provide reliable environmental predictions. In Greece, the available forecasts, although satisfactorily describe the overall picture in large or moderate scale, pose considerable problems to local weather information. These difficulties are magnified in areas of complex orography and coastline - characteristics of the Greek region.
To address these problems, the use of optimization techniques will be employed based on a relatively new branch of mathematics the Information Geometry. The latter implements techniques from the non-Euclidean Geometry in Statistics, targeting to the optimization of the solution of nonlinear problems.
One of the key issues is the appropriate estimation of the "distance" between two distributions or data sets. The classical treatment of such problems is usually based on regression techniques least squares methods. However, such an approach carries the assumption that the data processed belongs to an Euclidian - finite dimensional space.
Within the framework of Information Geometry it is proved that this is not always the case since a family of distributions is a manifold – i.e. a generalization of an Euclidean space - where the geometric properties may be quite distant from the classic. Thus, determining the necessary tools leading to the safe estimation of the geometric properties requires the construction of a Riemannian structure. The distances in such a complex environment are closely connected with the curves of minimum length (geodesics). The evaluation of the latter is equivalent to solving differential equations of second order.In classical Euclidean geometry these equations have always the form
![]()
which requires zero curvature and resolved in a segment. In the case of a non-Euclidean space M the corresponding requirement leads to a system of differential equations
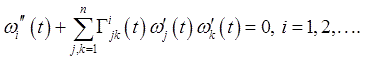
with boundary conditions:
![]()
where
![]()
is the desired curve of minimum length.
The form of these equations and their solutions, depending heavily on the functions that characterize the geometric properties of M are connected with the distribution followed by the data in study: usually the Gamma, the Normal or the Weibull distribution prove to be the optimal choices.
In most cases the determination of the analytic solutions of the differential equations obtained is not possible and the need for using approximate-numerical methods is imperative. The differential equations that should be solved are second order boundary value problems (BVPs). The numerical methods solving these equations must take into consideration the nature of the problem. In this respect, new optimization technique proposed will be based on the minimization of the computational cost which will take into account the geometry of the distributions space.
The new techniques and methodologies proposed in this project will be applied in selected areas of Greece where the use of renewable energy sources is of increased interest. Hopefully, the obtained results will provide the necessary information for the development of profitable renewable sources installations in these areas.
|