Numerical Solution of Periodic Media Problems

joint work with

C. Zheng, Tsinghua University, Beijing, China

H. Han, Tsinghua University, Beijing, China

J. Sun, Delaware State University, Dover, USA

Summary

Periodic structure problems often arise in science and engineering and often they are modeled by partial differential equations (PDEs) with periodic coefficients and/or periodic geometries. Periodic structure problems exist in modern applications of semiconductor nanostructures (e.g.\ quantum dots and nanocrystals), semiconductor superlattices, photonic crystal structures, meta materials with negative refractive indices or Bragg gratings of surface plasmon polariton wave guides. In order to numerically solve these equations efficiently one usually confines the spatial domain to a bounded computational domain (in a neighborhood of the region of physical interest).

The usual strategy is to introduce so-called artificial boundaries and impose adequate boundary conditions [1]. For wave-like equations, the ideal boundary conditions should not only lead to well-posed problems, but also mimic the perfect absorption of waves traveling out of the computational domain through the artificial boundaries.

First we present a novel analytical impedance expression is presented for general second order ODE problems with periodic coefficients [2] and its validity is shown to be strongly supported by numerical evidences. This new expression for the kernel of the Dirichlet-to-Neumann mapping of the artificial boundary conditions is then used for computing the bound states of the Schrödinger operator with periodic potentials at infinity using an 8th order finite element method. Other potential applications are associated with the exact artificial boundary conditions for some time-dependent problems with periodic structures. 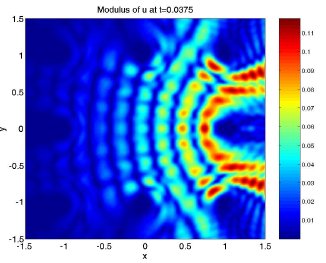As an example, a two-dimensional hyperbolic equation modeling the TM polarization of the electromagnetic field with a periodic dielectric permittivity is considered.

Secondly we design a new numerical technique for solving periodic structure problems [3]. This novel approach possesses several advantages. First, it allows for a fast evaluation of the Robin-to-Robin operator for periodic array problems. Secondly, this computational method can also be used for bi-periodic structure problems with local defects. Our strategy is an improvement of the recently developed recursive doubling process by Yuan and Lu. We will consider several problems, such as the exterior elliptic problems with strong coercivity, the time-dependent Schrödinger equation and finally the Helmholtz equation with damping and solve them with an 8th order finite element method. Let us note that the critical case when the wavenumber lies in the passbands is discussed concisely in [4].