|
Anton Arnold , Matthias Ehrhardt , Ivan Sofronov
Discrete transparent boundary conditions for the 1D Schrödinger equation
- scaled Schrödinger equation:
with
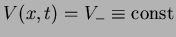 for for 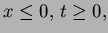
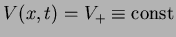 for for 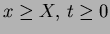
- goal: Solve the whole space problem (almost) exactly on the
computational interval
![$ [0,X]$](Exp_Sums/png/img11.png) by introducing transparent boundary conditions at by introducing transparent boundary conditions at
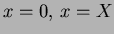 . .
- Crank-Nicolson finite difference scheme:
grid points:
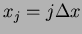 (with (with
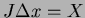 ), ),
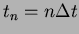
approximation:
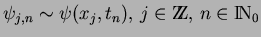 ; ;
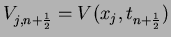
numerical scheme for whole space problem:
- discrete transparent boundary conditions:
(to be used with scheme (1) on
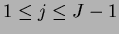 ) )
with convolution kernels
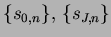 : :
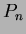 ... Legendre polynomials ( ... Legendre polynomials (
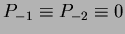 ) )
initial condition must satisfy:
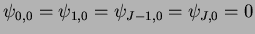
REMARK: The evaluation of the convolutions (2) is very expensive for large-time
calculations
 approximative "sum-of-exponential'' convolution
coefficients strongly reduce the numerical effort. approximative "sum-of-exponential'' convolution
coefficients strongly reduce the numerical effort.
- approximative transparent boundary conditions:
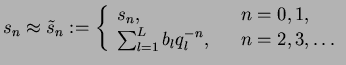 (3)
(3) |
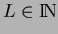 ... parameter to choose ... parameter to choose
Java-applet for calculation of 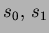 , ,
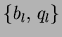 for given for given
download Maple-code for calculation of
- fast evaluation of discrete convolutions:
For the "sum-of-exponential'' convolution coefficients (3) the resulting
convolution in (2):
can be computed very efficiently by the algorithm:
where
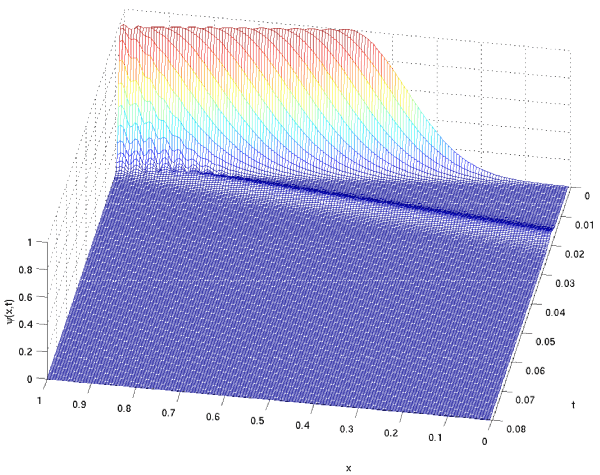
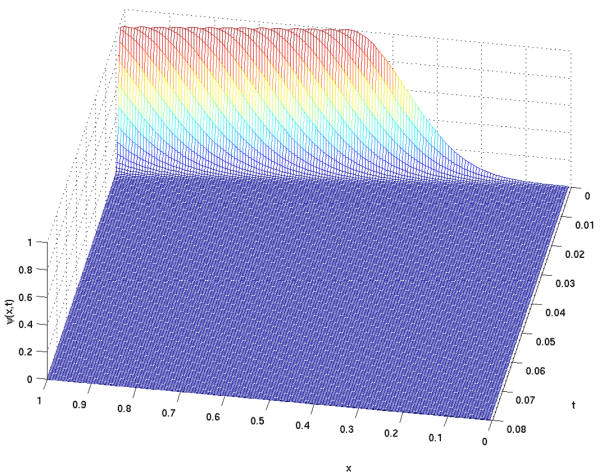
- example - free Schrödinger equation:
Gaussian beam, travelling right
Solution with L=10:
Solution with
L=20:
[Preprint: Arnold - Ehrhardt - Sofronov '02]
|





